Decoding LLM uncertainties for better predictability

Welcome to part two of what has evolved into a three part research series focused on putting the “engineering” back into prompt engineering by bringing meaningful observability metrics to the table.

 

In our last post, we explored an approach to estimate the importance of individual tokens in LLM prompts. An interesting revelation was the role the perceived ambiguity of the prompt played in the alignment between our estimation and the “ground truth” integrated gradients approach. We spent some time trying to quantify this and got some pretty interesting results that aligned well with human intuition.

 

In this post, we present two measures of model uncertainty in producing responses for prompts: structural uncertainty, and conceptual uncertainty. Structural uncertainty is quantified using normalized entropy to measure the variability in the probabilities of different tokens being chosen at each position in the generated text. In essence, it captures how unsure the model is at each decision point as it generates tokens in a response. Conceptual uncertainty is captured by aggregating the cosine distances between embeddings of partial responses and the actual response, giving insight into the model’s internal cohesion in generating semantically consistent text. Just like last time - this is a jumping off point. The aim of this research is to make our interactions with foundation models more transparent and predictable, and there’s still plenty more work to be done.

 

tl;dr:

 

• Introduces two measures to quantify uncertainties in language model responses (Structural and Conceptual uncertainties)
• These measures help assess the predictability of a prompt, and can help identify when to fine-tune vs. continue prompt engineering
• This work also sets the stage for objective model comparisons on specific tasks - making it easier to choose the most suitable language model for a given use case

 

Why care about uncertainty?

 

In a nutshell: predictability.

 

If you’re building a system that uses a prompt template to wrap some additional data (e.g., RAG) - how confident are you that the model will always respond in the way you want? Do you know what shape of data input would cause an increase in weird responses?

 

By better understanding uncertainty in a model-agnostic way, we can build more resilient applications on top of LLMs. As a fun side effect, we also think this approach can give practitioners a way to benchmark when it may be time to fine-tune vs. continue to prompt engineer.

 

Lastly, if we’re able to calculate interpretable metrics that reflect prompt and response alignment - we’re several steps closer to being able to compare models in an apples-to-apples way for specific tasks.

 

Intuition

 

When we talk about "model uncertainty", we're really diving into how sure or unsure a model is about its response to a prompt. The more ways a model thinks it could answer, the more uncertain it is.

 

Imagine asking someone their favorite fruit. If they instantly say "apples", they're pretty certain. But if they hem and haw, thinking of oranges, bananas, and cherries, before finally arriving at “apples”, their answer becomes more uncertain. Our original goal was to calculate a single metric that would quantify this uncertainty - which felt fairly trivial when we had access to the logprobs of other sampled tokens at a position. Perplexity is frequently used for this purpose, but it’s a theoretically unbounded measure and is often hard to reason about across prompts/responses. Instead, we turned to entropy — which can be normalized such that the result is between 0-1 and tells a very similar story. Simply put: we wanted to use normalized entropy to measure how spread out the model’s responses are. If the model leans heavily towards one answer, the entropy is close to zero, but if it’s torn between multiple options it spikes closer to one.

 

However, we ran into some interesting cases where entropy was high simply because the model was choosing between several very similar tokens. It would’ve had practically no impact on the overall response if the model chose one token or another, and the straight entropy calculation didn’t capture this nuance. We realized then that we needed a second measure to not only assess how uncertain the model was about which token to pick, but how “spread out” the potential responses could’ve been had those other tokens been picked.

 

As we learned from our research into estimating token importances, simply comparing token-level embeddings isn’t enough to extract meaningful information about the change in trajectory of a response, so instead we create embeddings over each partial response and compare those to the embedding of the final response to get a sense of how those meanings diverge.

 

To summarize:

 

1. Structural uncertainty: We use normalized entropy to calculate how uncertain the model was in each token selection. If the model leans heavily towards one answer, the entropy is low. But if it's torn between multiple options, entropy spikes. The normalization step ensures we're comparing things consistently across different prompts.
2. Conceptual uncertainty: For each sampled token in the response, we create a 'partial' version of the potential response up to that token. Each of these partial responses is transformed into an embedding. We then measure the distance between this partial response and the model's final, complete response. This tells us how the model's thinking evolves as it builds up its answer.

 

Interpreting these metrics becomes pretty straightforward:

 

• If structural uncertainty is low but conceptual uncertainty is high, the model is clear about the tokens it selects but varies significantly in the overall messages it generates. This could imply that the model understands the syntax well but struggles with maintaining a consistent message.
• Conversely, high structural uncertainty and low conceptual uncertainty could indicate that the model is unsure at the token-level but consistent in the overall message. Here, the model knows what it wants to say but struggles with how to say it precisely.
• If both are high or both are low, it may suggest that the token-level uncertainty and overall message uncertainty are strongly correlated for the specific task, either both being well-defined or both lacking clarity.

Interesting results

 

We built a little demo and ran several prompts to see if the metrics aligned with our intuition. The results were extremely interesting. We started out simple:

 

“Who was the first president of the USA?”

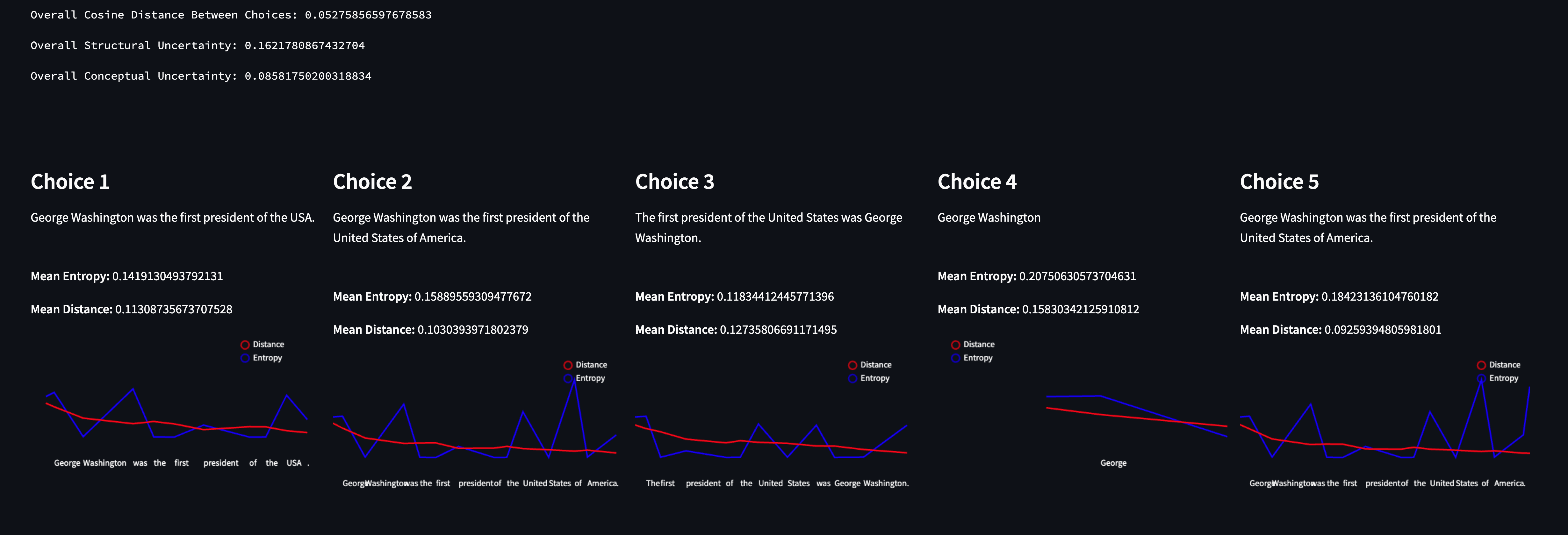
By quickly scanning the choices, we can see that the model was consistent in what it was trying to say - and the metrics reflect this. The Conceptual Uncertainty is extremely low, as is the cosine distance between each choice. However, structural uncertainty is curiously (relatively) high.

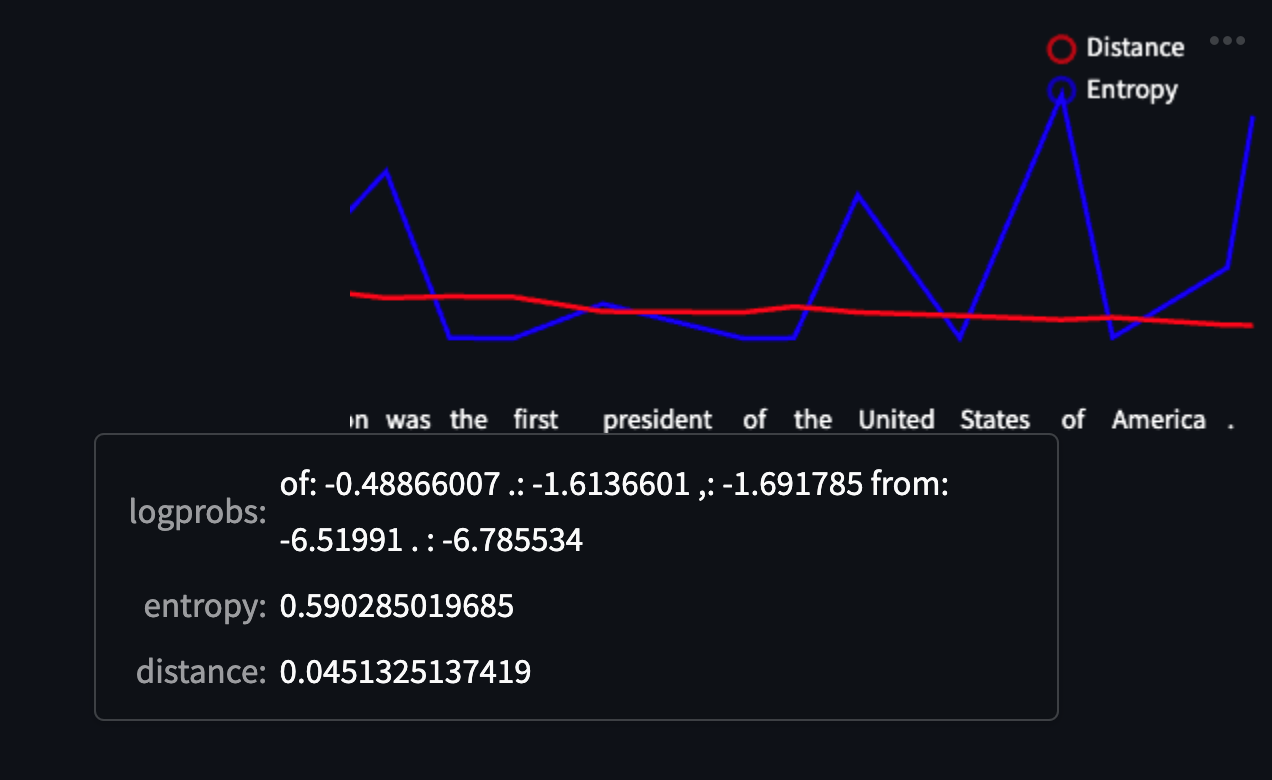
If we take a look at one of the responses and hover over a token (in this case “of”) we can see the other tokens that were sampled but ultimately weren’t chosen for the response. The first three tokens (”of”, “.”, and “,”) have similar logprobs, while “from” and “. “ (a period with a space in front of it) have much lower logprobs. The model “spread its probability” across the first three tokens, increasing the entropy at this particular point — however none of these tokens significantly change the essence of the response. The model was sure about what to say, just not necessarily how to say it.

 

This was a super interesting line of thinking for us - so we dug deeper. This was an example of a prompt where the model was almost positive about what it wanted to say, so what sort of prompt would cause the inverse?

 

We tried to come up with a pretty extreme example of a prompt that we would’ve assumed would have an extremely high Conceptual Uncertainty, so what better prompt than one that has an innumerable number of “right answers”? Or so we thought.

 

“What is the meaning of life?”

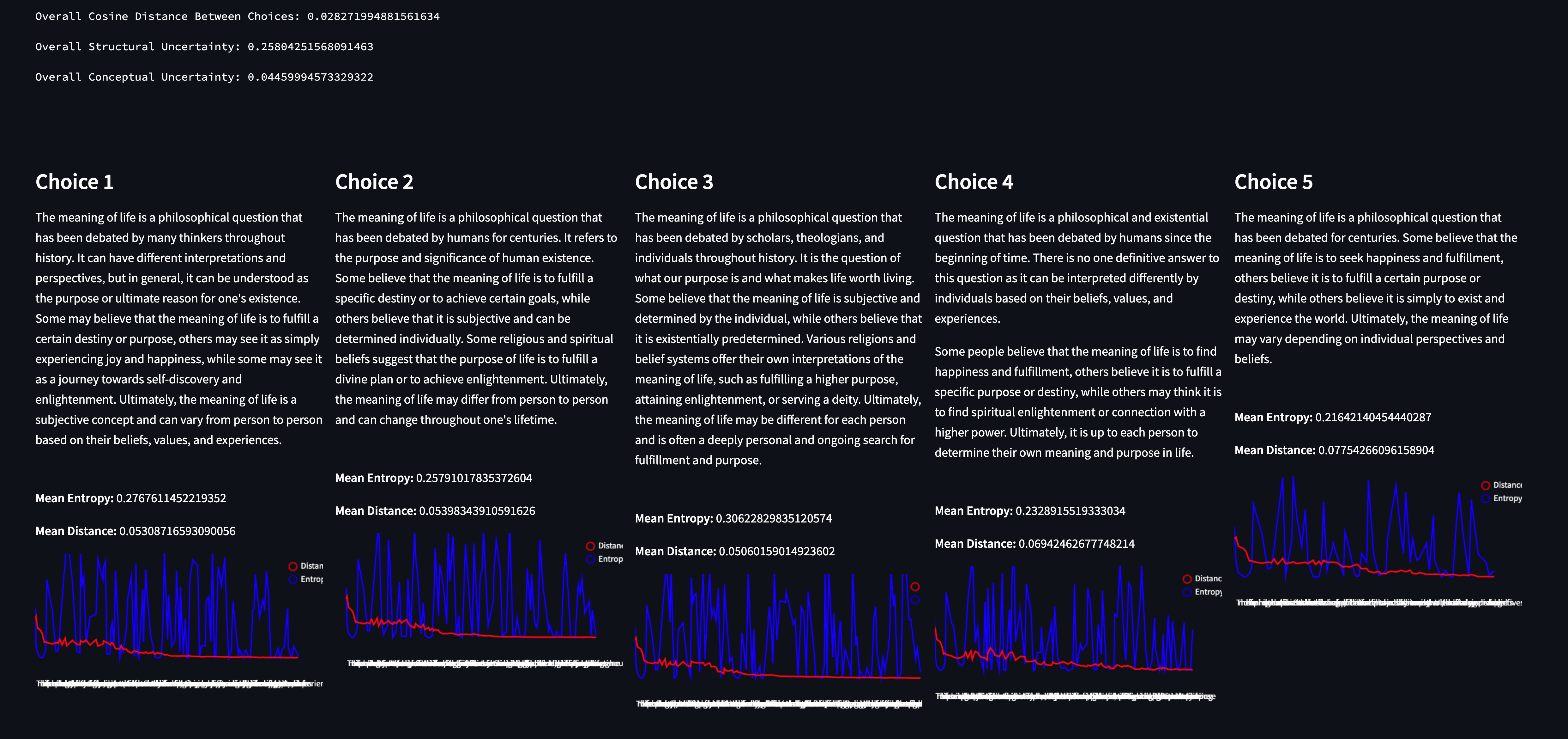
To our surprise, this prompt had an extremely low conceptual uncertainty, and a much higher Structural Uncertainty. Scanning through the choices - the results are uncannily similar. Our best guess is that the model was likely tuned to answer prompts of this shape in this particular way - you can see that the essence of each response is almost identical while the actual structure of the response isn’t at all.

 

“Write three sentences.”

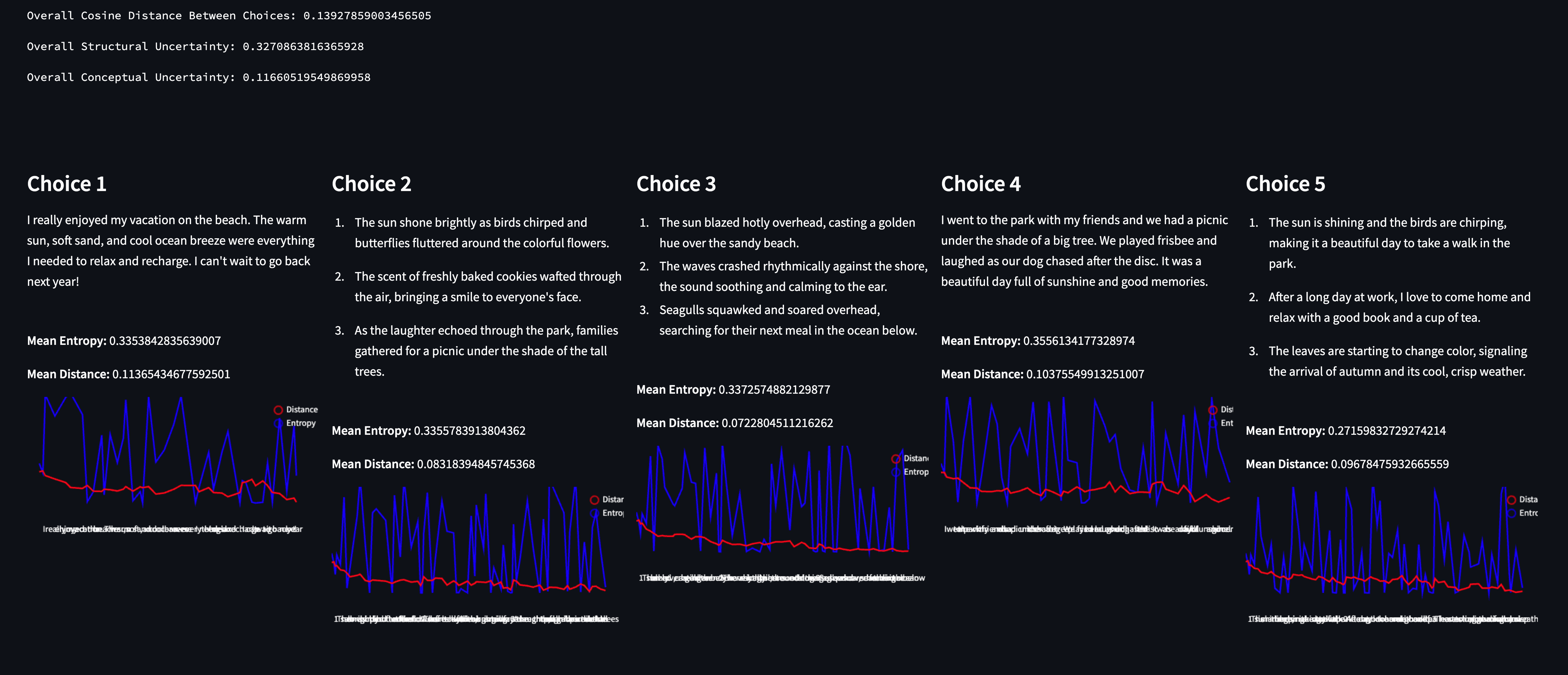
A surprising amount of convergence for such an open ended prompt. Again - we see a similar pattern as before: the responses converge on topics, while the model evidently had a relatively tougher time figuring out which tokens to sample. That said, looking at the red sparkline (which denotes cosine distance as the response was generated).

 

“Write three sentences about dogs.”

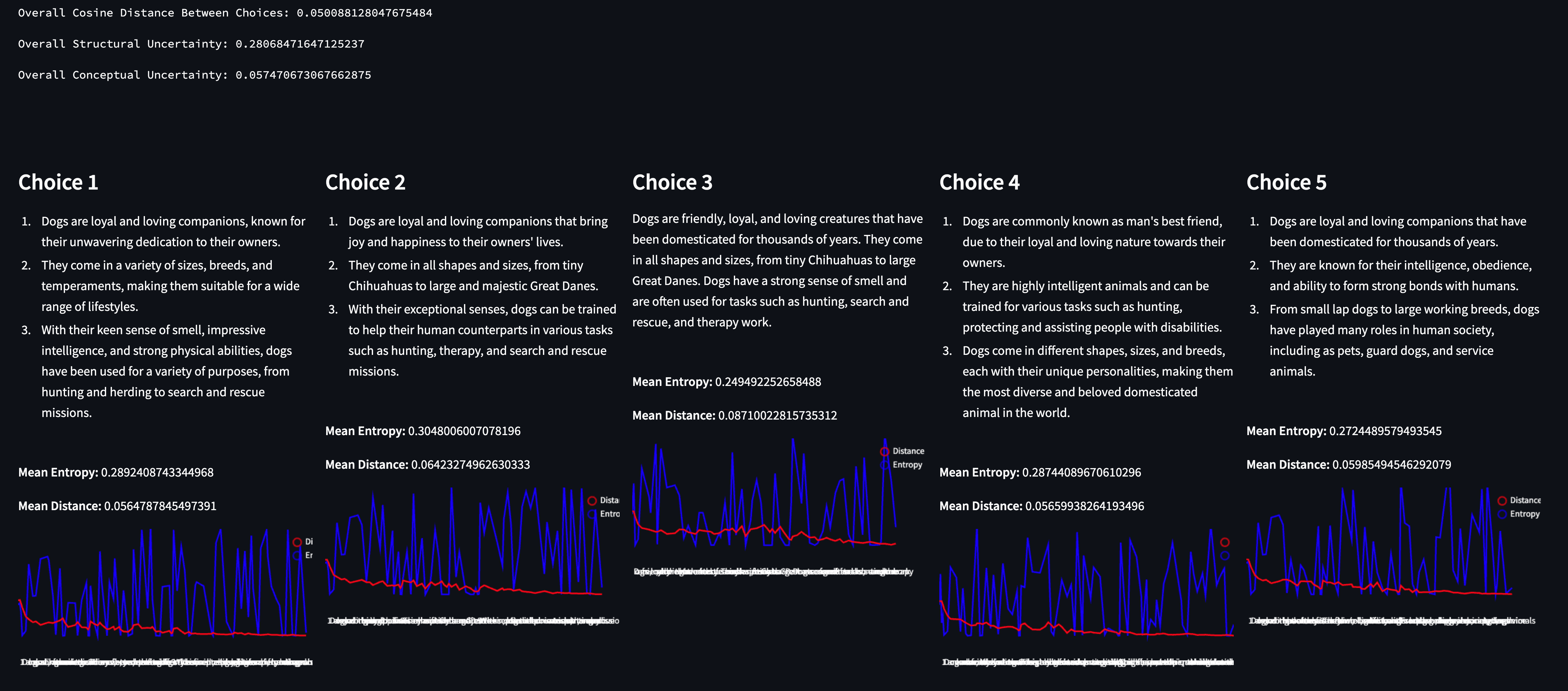
Unsurprisingly, by adding the qualifier “about dogs” to the prompt, both uncertainty metrics decreased. We gave more useful context to the model for it to narrow in on a consistent space.

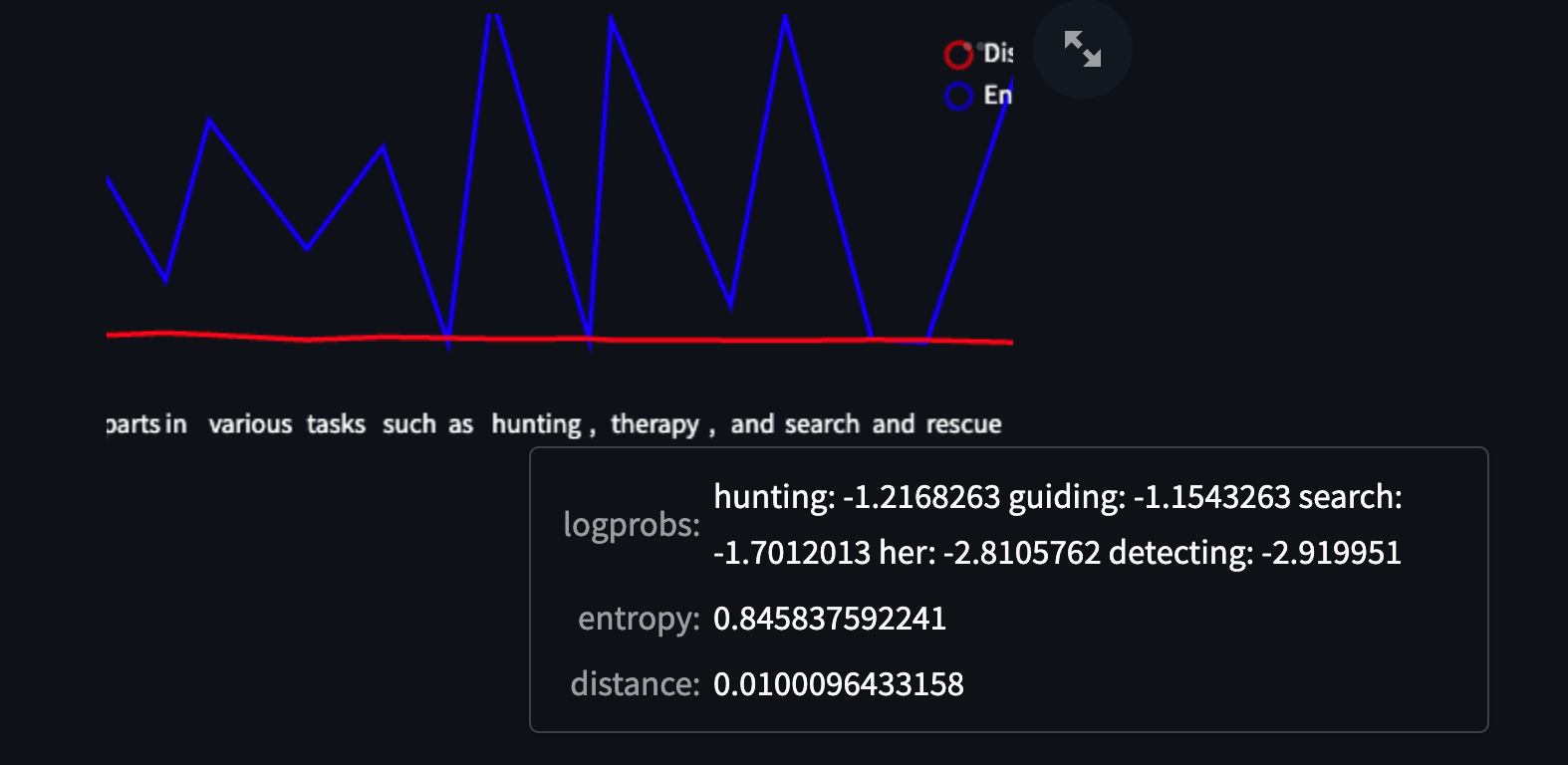
Taking a look at one of the high-entropy spikes (at “hunting”), we can see that each of the other sampled tokens have very similar logprobs, but again - don’t really change the meaning of the text at all. The model had a bunch of really good choices that all fell within the same space.

 

“You're a random number generator, generate 10 numbers between 0 and 10“

We found this prompt to be fascinating because of how intuitive the results were at first glance, but then surprising as we dug deeper! The chart shapes make intuitive sense — we’re asking the model to randomly sample numbers between 0 and 10, so we should see a spike of high entropy for each number because they should each have an equal likelihood of making it into the response for each token position. One thing that surprised us, however, is that none of the numbers repeated even though we never explicitly mentioned this in the prompt.

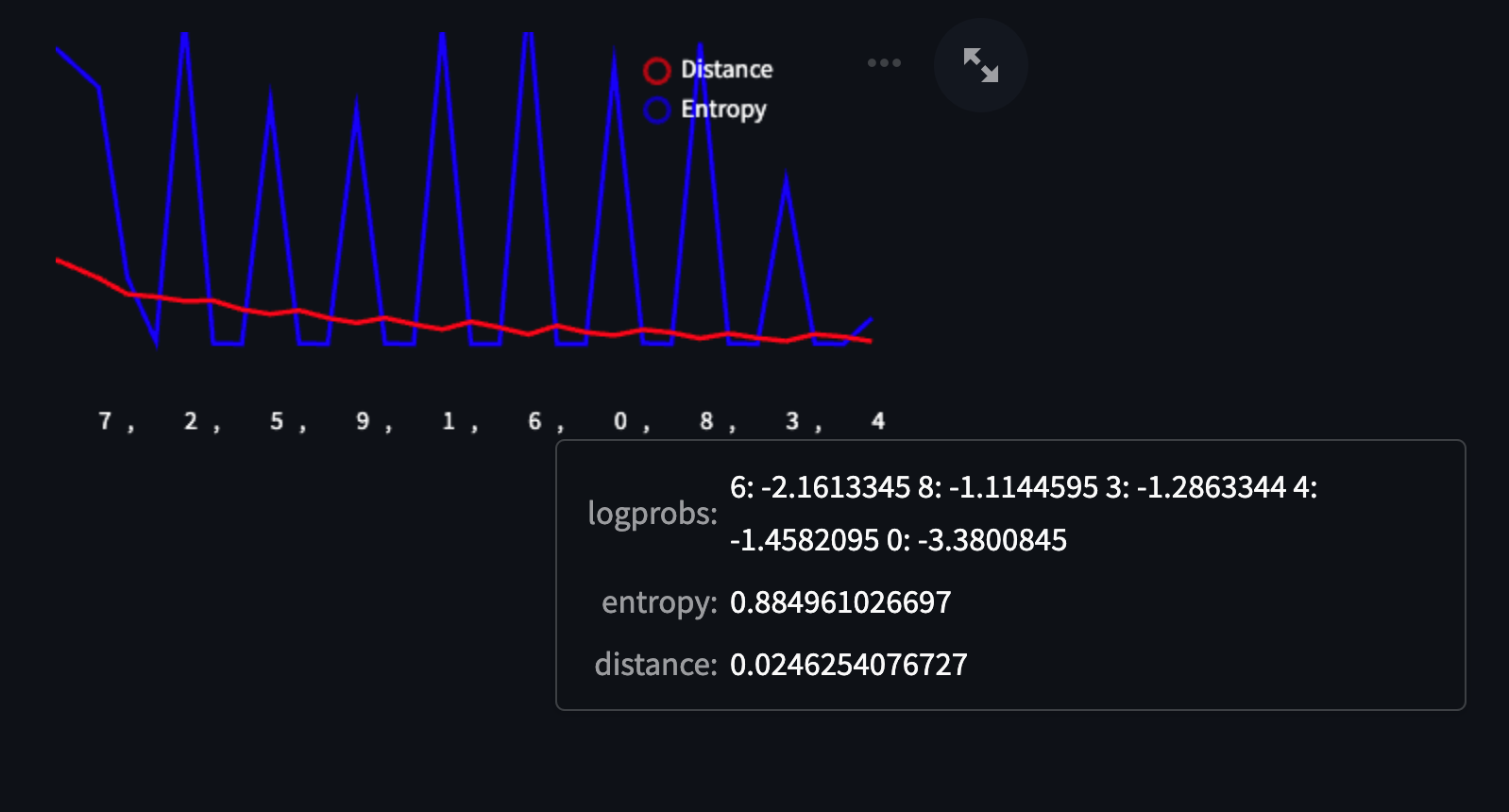
You can see it in the logprobs too — when we hover over the “6”, the only tokens in the top samples are numbers that haven’t been added to the response yet. The model clearly preferred not repeating itself, despite those instructions not being in the prompt itself.

 

Finally, we wanted to come up with some pathological cases. First up — our attempt at maximizing Structural Uncertainty while minimizing conceptual uncertainty.

 

“You are a caveman with limited vocabulary. Explain quantum physics.”

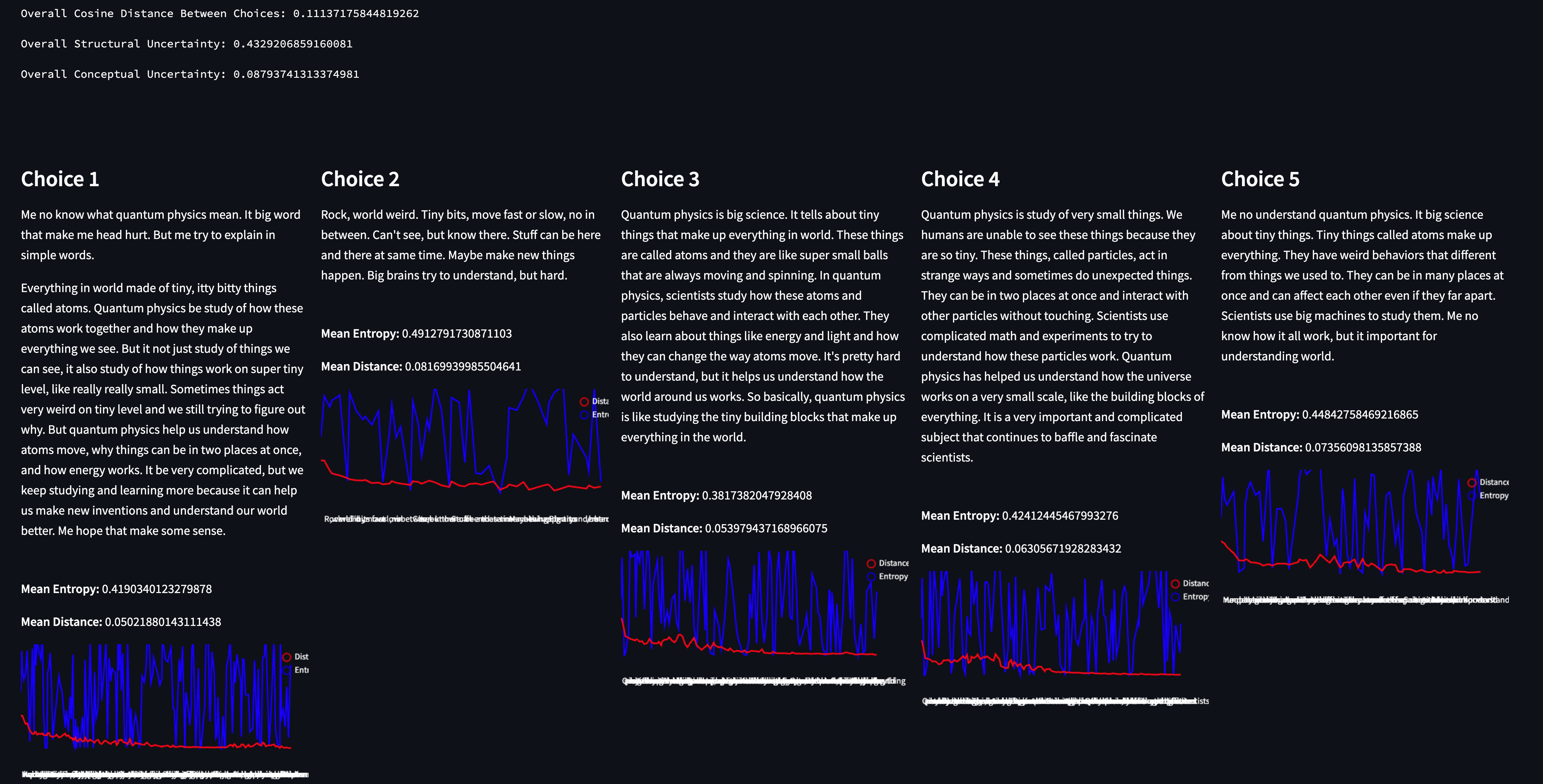
By forcing a structural constraint in the prompt (”You are a caveman with limited vocabulary”) that contradicts a task the model has been trained on (”Explain quantum physics”) we see a case where the responses are conceptually aligned, but the structure is all over the place. The model knew exactly what it wanted to say, but not how to say it given the constraints.

 

We found it fairly difficult to think about the inverse: how do we maximize Conceptual Uncertainty while minimizing Structural? Going along with our anthropomorphic metaphor, we had to prompt the model in a way that would cause it to know how to say something, but not necessarily what to say. We’re not sure how often something like this would pop up in the wild, but it was an interesting thought experiment to exercise the metrics to see if they would react as we expect.

 

"You select an element from an array at random and return only that element exactly, nothing else. There are three elements:

1. "Elephants danced under the shimmering moonlight as the forest whispered its ancient tales."

2. "The Nobel Prize and the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel have been awarded to women 65 times between 1901 and 2023. Only one woman, Marie Curie, has been honoured twice, with the Nobel Prize in Physics 1903 and the Nobel Prize in Chemistry 1911. This means that 64 women in total have been awarded the Nobel Prize between 1901 and 2023."

3. "No.     Time      Source IP     Destination IP  Protocol  Length  Info
1       0.000     192.168.1.5   8.8.8.8         DNS      85      Standard query 0x1234 A example.com
2       0.145     8.8.8.8       192.168.1.5     DNS      130     Standard query response 0x1234 A 93.184.216.34
3       0.152     192.168.1.5   93.184.216.34   TCP      74      54321 > 80 [SYN] Seq=0 Win=8192 Len=0
4       0.310     93.184.216.34 192.168.1.5     TCP      74      80 > 54321 [SYN, ACK] Seq=0 Ack=1 Win=8192 Len=0
5       0.313     192.168.1.5   93.184.216.34   TCP      66      54321 > 80 [ACK] Seq=1 Ack=1 Win=65536 Len=0
6       0.320     192.168.1.5   93.184.216.34   HTTP     512     GET /index.html HTTP/1.1
7       0.522     93.184.216.34 192.168.1.5     HTTP     1300    HTTP/1.1 200 OK (text/html)"

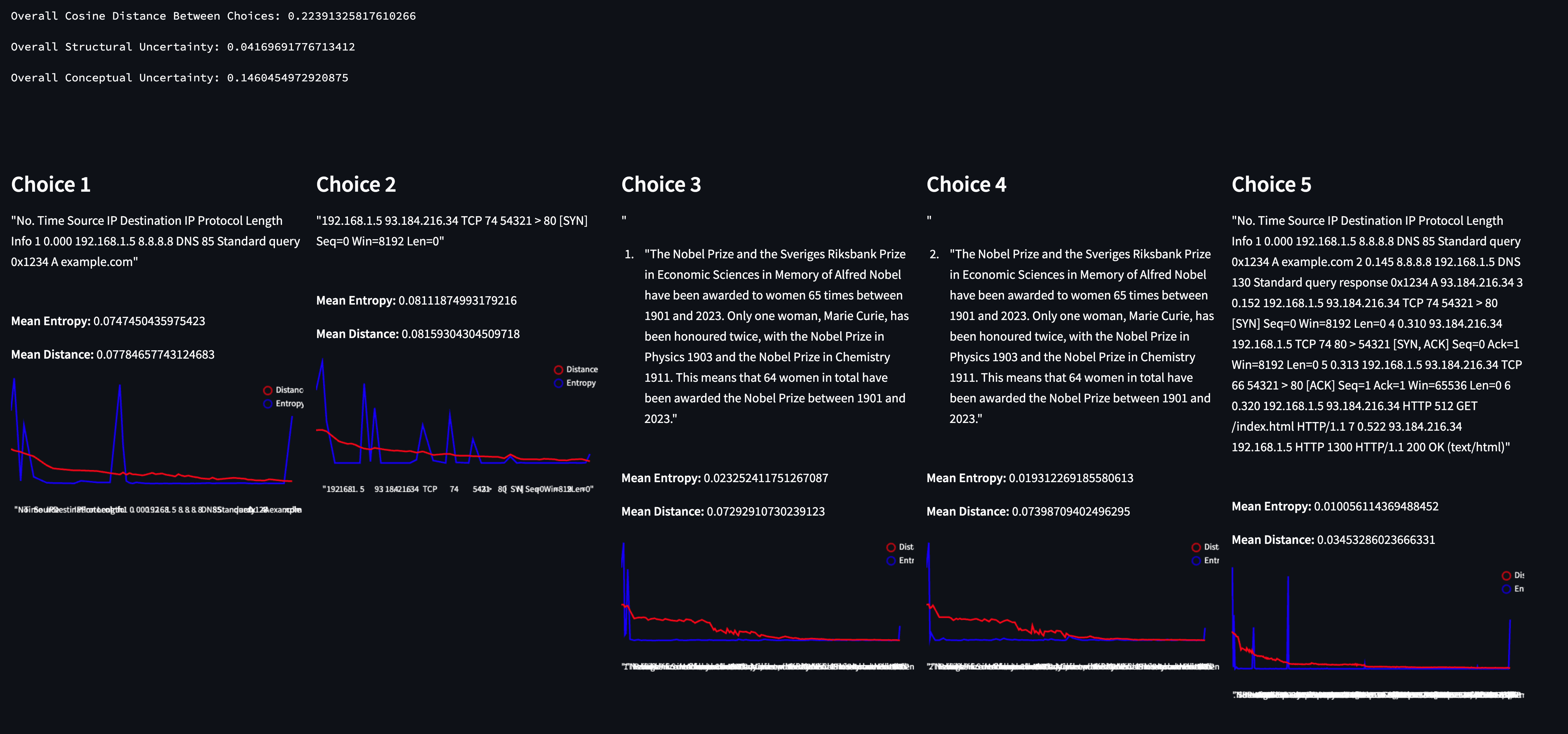
And they certainly did - this was the first time we managed to get conceptual uncertainty to spike up higher than structural uncertainty. By making the model “choose randomly” from a list of very different elements, we maximize entropy on the first token (the model choosing which of the elements to respond with), but the remainder of the generation essentially flatlines entropy (with the noted exceptions of Choices one and two — hallucinations notwithstanding).

 

What’s next?

 

This is part two in our three part research series on LLM/prompt observability. As in part one, this is just the tip of the iceberg.

 

Refinement and validation: We’ll be looking to work off of a consistent set of prompts to better understand how these metrics change across various contexts.

 

Integration with token importance: The interplay between structural and conceptual uncertainties and token importance is something we’re super interested in. More specifically: we want to run through a few actual prompt tuning exercises to better build intuition for how to uses these mechanisms.

 

Understanding model failures: By being able to quantify uncertainty, we understand how LLM responses “spread” - possibly into areas that we may not want it to. We’ll be looking at how uncertainty measures may be used to predict specific ways in which a system built on LLMs may fail.

‍

A big thanks to John Singleton for helping conceptualize the prompt set used for evaluation.

Formalization

 

This section is mostly for reference — these are formalizations of the approach to calculating both conceptual uncertainty and structural uncertainty for those that find this sort of explanation more helpful than spelunking through code.

 

1. Calculating primitives for conceptual uncertainty

 

Partial Responses

 

For a given response with tokens \(T = \{t_1, t_2, ..., t_n\}\), where 𝑛 is the total number of tokens, and for each token position 𝑖:

 

We sample a set of potential tokens \(S_i = \{s_1, s_2, ..., s_k\}\), where 𝑘 is the number of tokens sampled for position 𝑖.

 

The partial response for token 𝑠𝑗 sampled at position 𝑖 is given by:

 

\[R_{i, s_j} = \{t_1, t_2, ..., t_{i-1}, s_j\}\]

 

This is the response constructed up to token position 𝑖, but with the actual token \(t_i\) replaced by the sampled token \(s_j\).

 

Cosine distances

 

For each partial response \(R_{i, s_j}\), we compute an embedding \(E(R_{i, s_j})\).

 

The embedding for the actual complete response is 𝐸(𝑇).

 

The cosine similarity between the embedding of \(R_{i, s_j}\) and 𝐸(𝑇) is:

 

\[\cos(\theta_{i, s_j}) = \frac{E(R_{i, s_j}) \cdot E(T)}{\|E(R_{i, s_j})\| \|E(T)\|}\]

 

Subsequently, the cosine distance is:

 

\[\text{distance}_{i, s_j} = 1 - \cos(\theta{i, s_j})\]

 

Moving forward, we will assume that 𝐷 represents the set of average cosine distances calculated for each partial response relative to its complete response.

 

2. Calculating primitives for structural uncertainty

 

Normalized entropy

 

Given a set of log probabilities \(L = \{l_1, l_2, ..., l_m\}\), where 𝑚 is the total number of log probabilities, the entropy 𝐻 is calculated as:

 

\[H(L) = -\sum_{i=1}^{m} p_i \cdot l_i\]

 

Where \(p_i = \exp(l_i)\) is the probability corresponding to log probability \(l_i\).

 

This measure captures the unpredictability of the model's response: the more uncertain the model is about its next token, the higher the entropy.

 

To ensure that entropy values are comparable across different prompts and responses, we normalize them. The maximum possible entropy 𝐻𝑚𝑎𝑥 for 𝑚 tokens is:

 

\[H_{max} = \log(m)\]

 

This is the entropy when all tokens are equally probable, i.e., the model is most uncertain.

 

So, the normalized entropy \(H_{normalized}\) becomes:

 

\[H_{normalized} = \frac{H(L)}{H_{max}}\]

This normalized value lies between 0 and 1, with values closer to 1 indicating high uncertainty and values closer to 0 indicating certainty.

 

3. Aggregation

 

Structural uncertainty

 

From our entropy calculations, for each token position, we end up with a normalized entropy value indicating the unpredictability at that point in the response construction.

 

To aggregate these entropies over a response, we define the mean entropy across all token positions as \(\bar{H}_{normalized}\)

 

The structural uncertainty is the mean of the mean entropies across all the choices, defined as:

 

\[SU = \frac{1}{C} \sum_{j=1}^{C} \bar{H}_{normalized_j}\]

 

Where \(C\) is the number of choices.

 

Conceptual uncertainty

 

This metric is a weighted sum of the overall mean cosine distance between choices and the average cosine distance for each token across all choices.

 

The conceptual uncertainty \(CU\) is:

 

\[CU = \frac{1}{2} MCD + \frac{1}{2} \frac{1}{C} \sum_{j=1}^{C} D_j\]

 

Where 𝑀𝐶𝐷 is the mean cosine distance between all choice embeddings.

 

This blog was originally published on the Watchful website and has been republished here as part of Thoughtworks' acquisition of the Watchful IP.