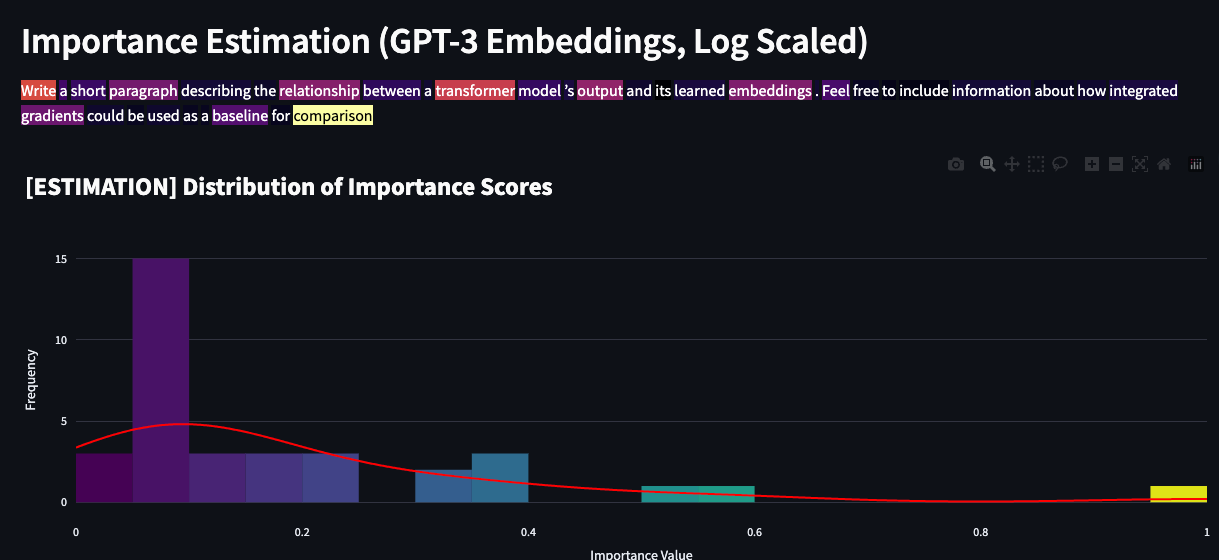

You can play with a demo here. Repo along with analysis notebook can be found here.
The increasing importance of LLM prompts
As we find ourselves interacting more frequently with large language models like ChatGPT, the way we prompt these models becomes increasingly important. Prompting is our primary means of instructing these AIs, yet the process of crafting effective prompts has largely been rooted in more art than science. While we've seen some strategies emerge, such as "meta-prompts," these often yield inconsistent results. Given that most users don't have access to the internal workings of these models, there's a need for tools that offer some level of interpretability.
In this blog post, we explore one such tool — a method for gauging the importance of individual tokens within prompts using text embeddings. This is more of a proof-of-concept for now, there are a lot of improvements to be made — we have lots of ideas on how to build on this idea and are excited to explore its full potential with the community.
Methodology
The hypothesis here is that there is a relationship between the embeddings of a prompt and how the model interprets it so long as there are architectural similarities between the embedding model and target model. A big caveat is that there are a lot of implicit assumptions being made along the way, such as
Architectural alignment. the definition of “similar architectures” is not rigorous. In this case, we tested against a GPT-2 model and ada-002 embedding model — the second of which we know very little about in terms of architectural details.
Embedding sensitivity. it’s assumed that the embeddings are sensitive enough to exhibit noticeable changes when perturbations are made to prompts.
Model capability. It’s likely that by testing against a more capable model than GPT-2 we would see even higher correlation — it’s possible that the “ground truth” used in this experiment was suboptimal.
We’re planning on doing a more foundational test of this approach across several model architectures, embeddings, etc. — but figured the results were already promising enough to start a conversation.
To begin with, we wanted to test the simplest possible implementation:
Tokenization: Break the prompt down into its individual words or 'tokens.'
Text embedding: Convert the text prompt into a numerical format, known as an 'embedding.'
Ablation and re-embedding. Remove each token one by one, create a new embedding, and then compare it to the original.
Importance estimation. The degree of difference gives us a rough idea of each token's importance.
Experimental structure
We tested our approach against Integrated Gradients attributions on GPT-2, as it’s a well-established and widely accepted method for attributing the contribution of individual input features (tokens in this case) to a model’s prediction. Imagine a model as a black box with many knobs (features) on it. By adjusting these knobs from a baseline (starting point) to their actual values and observing the change in output, Integrated Gradients tells us how much each knob's adjustment contributed to the final decision. It's like tracing back the decision-making process to see which features played the most significant roles — but as a result it requires access to model internals which is generally out of scope for most popular LLMs today.
We tested 5 prompts across two main configurations:
GPT-2 embeddings <> GPT-2 Integrated Gradients
GPT-3 (ada-002) embeddings <> GPT-2 Integrated Gradients
GPT-2 Integrated Gradients was generally used as a ‘ground truth’ target, and we used Pearson Correlation and Cosine Similarity between the estimated importance scores and the attributions we get from integrated gradients to assess correlation. When comparing the two importance value vectors, we weren’t as interested in metrics that were sensitive to magnitude of the importance values (e.g: euclidean distance or Kendall’s tau) because there’s no guarantee that our estimations would be within the same scale of magnitudes from an integrated gradients approach.
Put simply:
With Pearson correlation we wanted to measure:
a. If tokens we estimated to be important were generally also found to be important by integrated gradients
b. If tokens we estimated not to be important were generally also found to be unimportant by integrated gradients
c. It’s possible that the relationship between the two datasets is non-linear (pearson correlation wouldn’t fully capture that). It’s not a be-all-end-all metric, but we conducted additional checks to ensure that it was generally reasonable to use in this case.
With Cosine similarity we wanted to measure whether the information being conveyed by our estimation was directionally similar to the information being conveyed by integrated gradients.
Some preliminary findings
We ran the experiment and got some pretty interesting results. The prompts we used can be found here.
The intention was to find prompts that increased in “ambiguity”. The first two are straight forward mechanical operations that provide context. The third prompt is long but includes several few shot examples, so the overall scope is relatively constrained. The fourth and fifth prompts reduce the number of examples further and also make the tasks more open ended. One future extension of this work is to be able to estimate prompt ambiguity/perplexity in a cheap way, but for now we took a more intuitive approach to introducing this concept into the experiment.
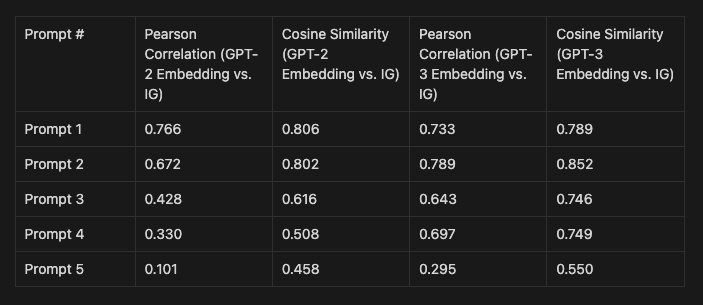

The majority of the prompts, especially when looking at the Pearson correlation and cosine similarity values, show a strong alignment between our embedding-based method and the Integrated Gradients approach. This consistency suggests that even with a rudimentary methodology, there's potential in using embeddings as a means of extracting operational insight into a model, especially when the actual internal workings of models are inaccessible. More directly, we’ve observed that these calculated “importances” can be a reasonable proxy/signal for attributions.
Prompt 5 stands out as an anomaly, hinting that the clarity of a prompt might heavily influence the accuracy of the estimation. This observation poses a fascinating question: How does the inherent ambiguity or clarity of a prompt affect the reliability of token importance estimates, and the fan-out of model interpretation? Delving deeper into this could pave the way for refining the approach, possibly by incorporating mechanisms to handle or account for ambiguous prompts.
The superior performance of GPT-3 embeddings, even when benchmarked against GPT-2, was surprising to us. It challenges our preconceived notion of architectural alignment being the linchpin for predictive accuracy. Instead, the intrinsic quality and robustness of embeddings emerge as being more significant. This raises another interesting question: Could other high-quality embeddings, even from non-GPT architectures, provide similarly reliable token importance estimations?
Ultimately, the correlation we’re seeing here surprised us given the simplicity of the approach. What’s more — our estimation is several orders of magnitude cheaper/faster to compute than the integrated gradients approach (don’t take our word for it, try it for yourself in the demo).
What we’ve learned so far
We’re seeing that there is in fact a relationship between the embeddings and model operation
We sometimes see a divergence in the model “ground truth” from the estimation (GPT-2 or GPT-3 embeddings).
We see that estimations from GPT-3 embeddings perform more optimally than GPT-2 embeddings
This may imply that the relationship is not based entirely on architectural alignment between the embedding space and the model it came from, but instead by the quality of the embeddings and the model.
Our guess is that if we run the integrated gradients approach on a more capable target model (e.g: GPT-3 or GPT-4) we may see better alignment.
We’re fairly confident that the results we’ve seen merit further investigation into the relationship between model outputs and embeddings, but the mechanisms we’re using here can definitely be refined further before being universally applicable. Here are a few areas of consideration for this approach as-is.
When it may be useful
High-quality embeddings. If the embeddings are robust, the token importance estimates tend to be more reliable.
Simple, unambiguous prompts. Clear and straightforward prompts are where this method seems to offer the most reliable results.
Areas for caution
Complex prompts. Ambiguity or complexity in the prompt can lead to less reliable estimates.
Atypical prompt lengths: For instance, very short or very long prompts. These results tend to still be correlated, but deviate a bit more than prompts of “average” length.
What comes next? Some thoughts
We see this work as a first step and are excited about the potential avenues for further research. Some immediate examples we already have in mind:
Refinements. Further calibration of the method to improve its reliability and correlation with ground truth attribution.
Broader testing. Applying this approach across various types of language models and tasks.
Entropy estimation. Given the fact that highly ambiguous prompts confound this type of approach, it would be interesting to be able to estimate how ambiguous a prompt actually is.
Once the approach is refined a bit more, it’s possible that it could be a reliable building block for a few interesting extensions:
Automatic prompt optimization. Experiment with dropping unimportant tokens from large prompts to reduce token spend.
Programmatic prompt improvement. If you’re able to estimate token-level importances with high fidelity, it provides a roadmap to the highest impact tokens that could be manipulated to change the outcome of a prompt. Having the importance values reduces the total space of manipulations to be performed and also helps prioritize them.
Ethical AI. Use the importances to help map out parts of prompts that might be introducing unintended bias.
One small step
We offer this method as a contribution to the broader effort to understand and interact effectively with large language models. While we're encouraged by our initial findings, we recognize that this is just one small piece of a much larger puzzle. We look forward to collaborating with the community to explore this and other methods further. We’ll likely release more of our code around this in the near future, so stay tuned for that.
This blog was originally published on the Watchful website and has been republished here as part of Thoughtworks' acquisition of the Watchful IP.
Disclaimer: The statements and opinions expressed in this article are those of the author(s) and do not necessarily reflect the positions of Thoughtworks.














